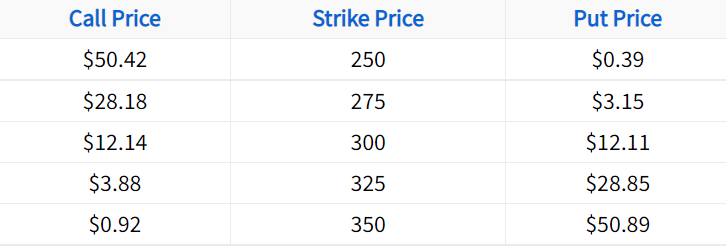
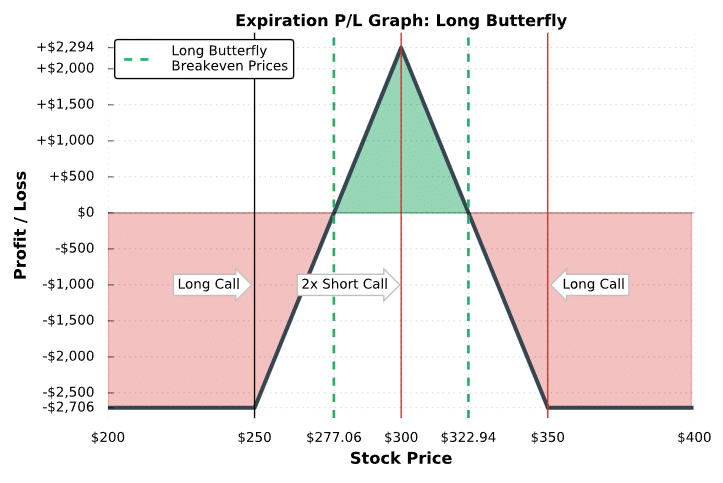
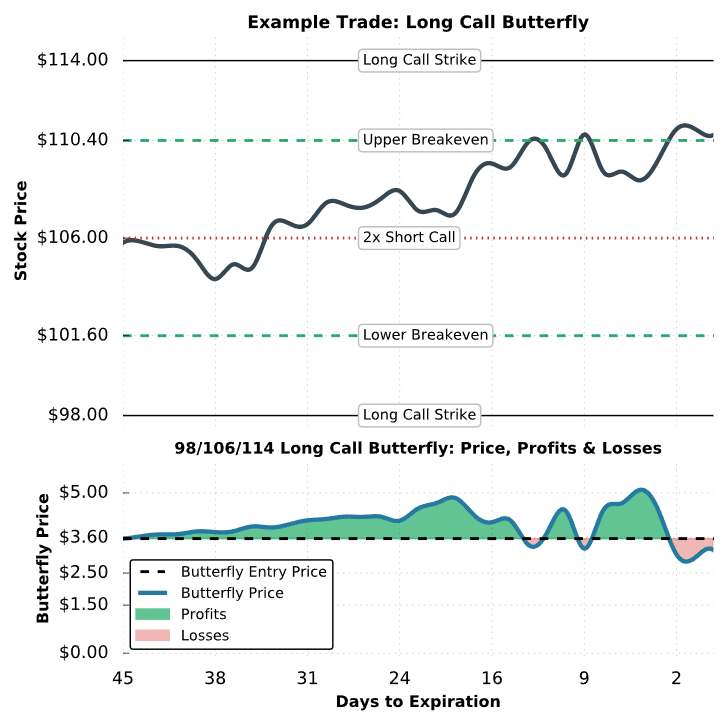
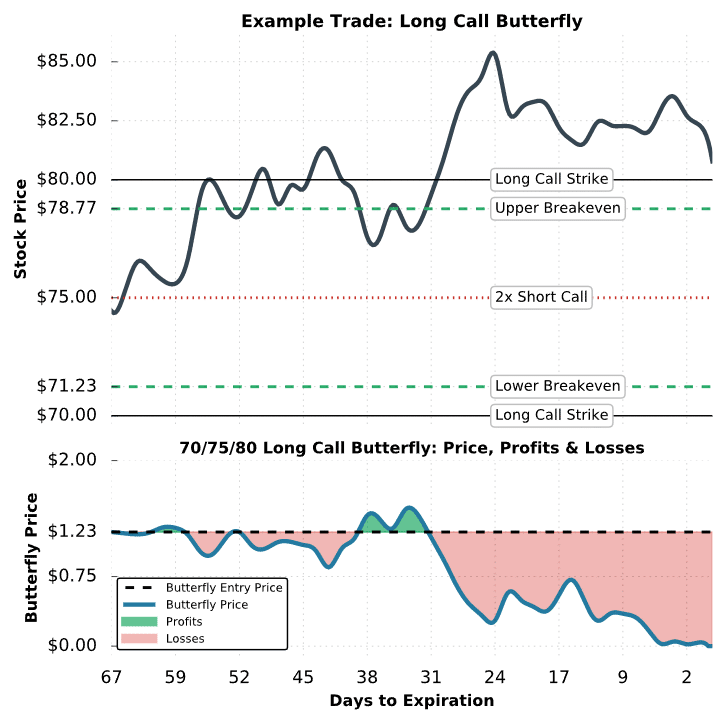
Last updated on February 10th, 2022 , 01:11 pm
Before you learn of shorting call and put options, you must first understand the basic components of these strategies. Let’s get started with learning about intrinsic and extrinsic value!
Intrinsic & Extrinsic Value
There are two components that make up the whole of an option’s price, known as Intrinsic & Extrinsic value. Let’s go through each of them one by one:
Intrinsic Value
If you’ve gone through the first part of this guide, you don’t know it yet, but you already understand what an intrinsic value represents in an option’s price.
We had a house example in the first part where the house was valued at $350,000, and we had a call option to buy it at a strike price of $200,000. In that example, since we could buy the house $150,000 less than its current value (a benefit of $150,000), the call is said to have an intrinsic value of $150,000.
It means that the option contract in the home example is worth at least $150,000 because we, as the owner, can use it for a benefit or profit of $150,000.
For put options, it’s the opposite. If you have a put option with a strike price of $130 while the stock price is at $120, you have a put contract that can sell stock $10 higher than its current value, meaning a profit of $10. This $10 is called the intrinsic value of the option.
To sum up, intrinsic value is the real value that an option can provide to its owner, and it is the minimum value of an option contract.
Extrinsic Value
The second component is called Extrinsic Value. An option’s extrinsic value is the portion of the option’s price that exceeds its intrinsic value. Let’s take an example to better understand it:
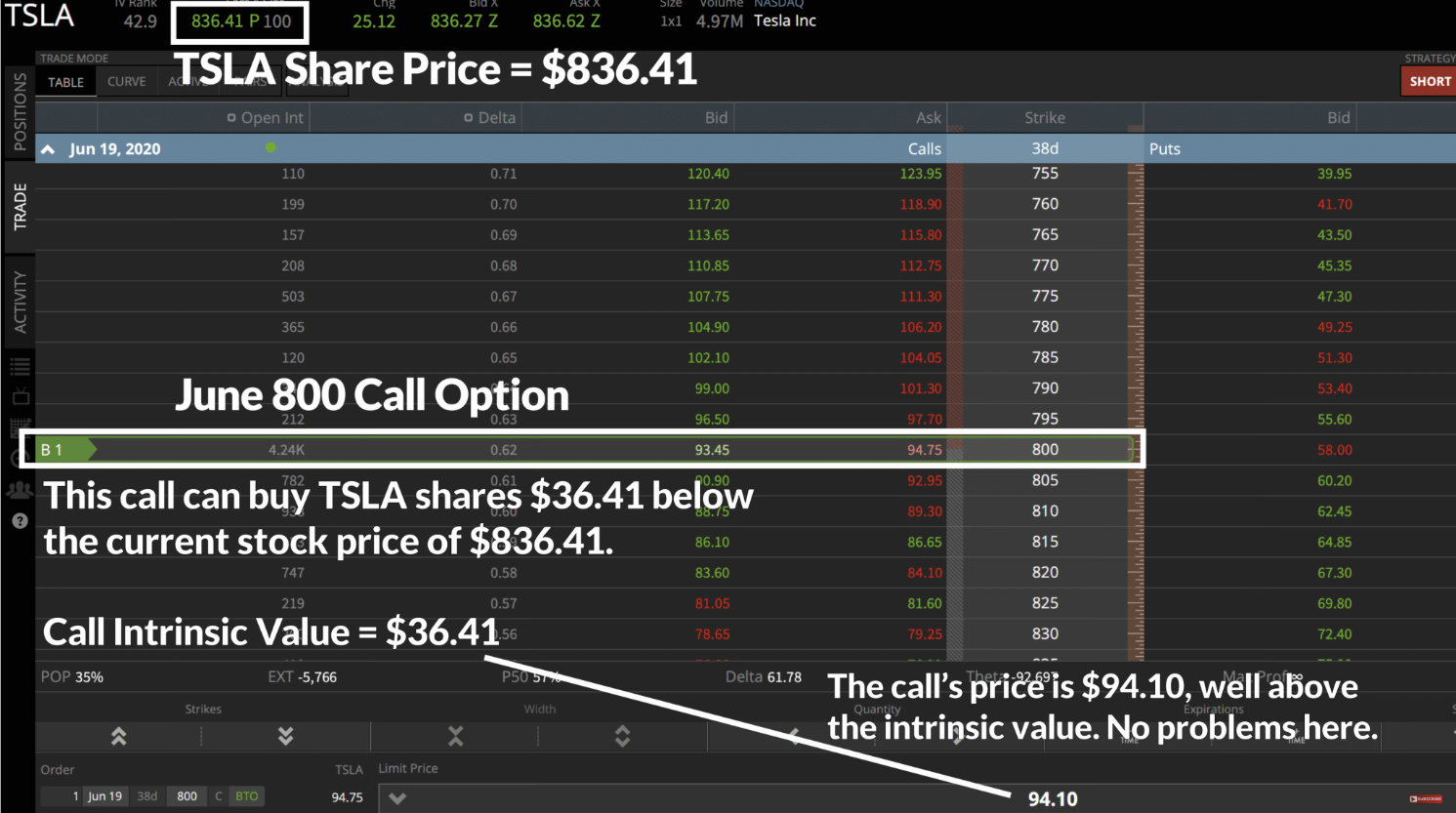
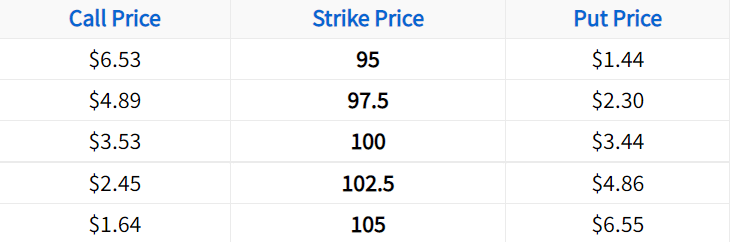
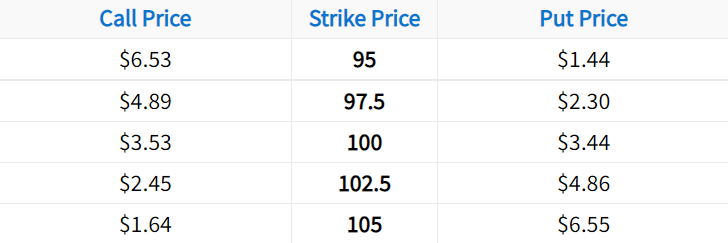
In the image above, TSLA is trading at a share price of $836.41 and we can see a call option with a strike price of $800. So as you can guess, the call option has an intrinsic value of $36.41, which is the benefit or real value it can provide to its owner. Why? Because the 800 call can be used to buy shares at $800/share, which is $36.41 below the current share price of $836.41.
But as we can see, the actual option price is $94.10, which is much higher than its intrinsic value. Here, the portion of the TSLA option’s price that is above its intrinsic value of $36.41 is called its extrinsic value.
We can understand an option’s extrinsic value as the part of its price associated with the potential for the option to become more valuable before its expiration. That is why the extrinsic value is sometimes referred to as “time value.”
As time passes, extrinsic value is lost, leaving only intrinsic value at expiration.
So in the case of this TSLA option, it has a 30-day expiration period. And going by TSLA’s volatility, we all know it can move around a lot in a 30-day period. So if TSLA ends up climbing to $900 by the option’s expiration date, its intrinsic value will increase to $100, which is why it makes sense that its current extrinsic value is $57.69.
This brings us to another point: options with a longer-term expiration date will trade with higher levels of extrinsic value compared to those with shorter expiration dates, because of the simple reason that with more time until expiry, stocks have larger potential movements.
In-the-Money (ITM), Out-of-the-Money (OTM), At-the-Money (ATM)
These are the three terms that you’ll get to hear often as an options trader, that’s why it’s important to cover them before we get to shorting options.
These terms essentially describe whether or not an option has intrinsic value or not. They represent the “moneyness” of an option.
In-the-money means any option with intrinsic value. So in our TSLA example, if the call’s strike price is $800 while the stock price is $836, the call has an intrinsic value of $36. Therefore, the call is said to be “in-the-money.”
Out-of-the-money is the exact opposite. Any option is said to be out-of-the-money when it has a 100% extrinsic value or no intrinsic value.
An example could be the IWM put option with a put strike price of $130 and a stock price of $130.71. The put option doesn’t have any intrinsic value in its price and therefore it is said to be an out-of-the-money put option.
The last term is at-the-money, which is when an option has a strike price equal to or very close to the current stock price.
Shorting Options
Shorting options can be confusing for beginners because here you’ll learn that we don’t always buy options, we can actually bet against them too. Betting against an option means that we put on a trade that profits when the option price falls.
If you know stock trading, then you probably know what shorting stocks is. It means that you sell the stock first at the current price without owning the shares, and then close your position by buying them back in the future, ideally at a lower price.
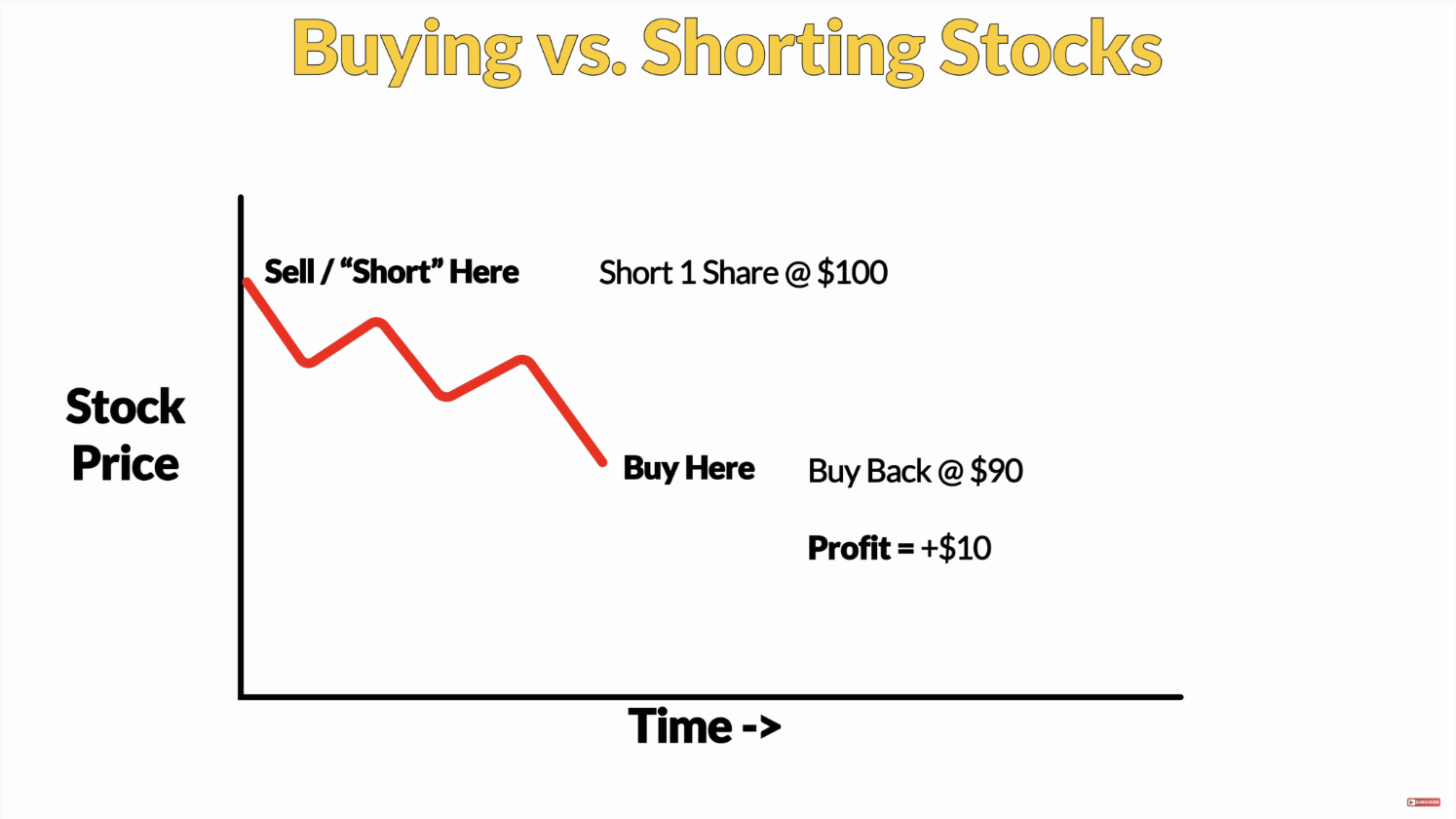
Shorting options is the same concept, but instead of stocks, you short options. You open your position by selling options you don’t own and your goal is to buy back the option at a lower price in the future.
So for example, say I short a call option for $5, meaning I collect a premium of $500 in my account, and later if the option price falls to $3, I buy back the option at a premium of $300, making a $200 profit on the trade.
Shorting Call Options With an Example
Let’s take a real-life example of shorting a call option to get a complete understanding of the subject:
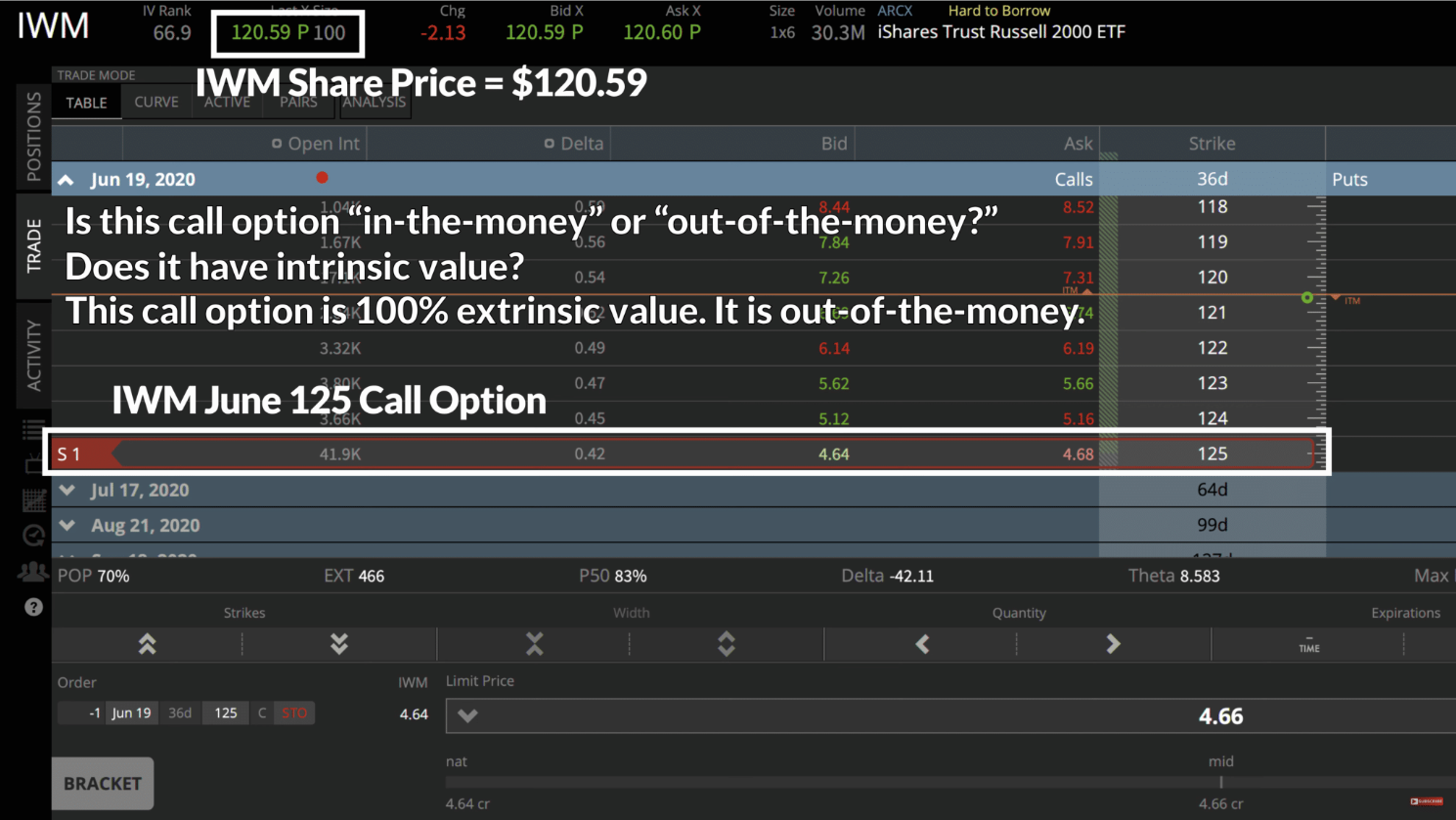
In the above image, we can see that the current share price of IWM is $120.59, and we look at shorting the June 125 call option (strike price of $125). The call option is 100% extrinsic value, meaning it is “out-of-the-money.” The option’s price is $4.66, which, again, is 100% extrinsic.
Now since we’re shorting options, I’ll not pay the $466 premium, rather I’ll collect it in my account, as we’re selling this option right now. But remember, collecting the money doesn’t mean it produces a profit. I’ll still have to buy it at a lower price to realize any profit.
Before we move forward, I must tell you that this is an extremely risky trade to enter. Because a call option’s price increases with the stock price, and since there’s no upper limit to how high a stock’s price can go, a call option also has no upper price limit. Therefore, “shorting a naked call option” like this trade has unlimited loss potential, in theory.
And since it is such a risky strategy, you’ll have to have a margin account. That means you have to be able to put collateral aside to enter the position. So the example that we’ve just seen above would require me to have $2,000 set aside in my account to bear potential losses if I want to short this call option.
Short Call Breakeven Price
Before we move forward, it is important to discuss the concept of the breakeven price and how it is possible to make money even if the stock price is above the call’s strike price. Say you short a call option in NFLX (Netflix) with a strike price of $400 and short it for $17 (you collect $1,700).
The breakeven price for this call trade is $417. But why? Because at expiration, an option will only have intrinsic value, if any. For a call option with a strike price of $400, the call will have $17 of intrinsic value if the stock price is at $417. If the stock price is at $417 at expiration, the call will be worth $17 (premium of $1,700). Since that’s the same as my initial sale price, I’d have no profit or loss if the option was worth $17 at expiration.
And so if NFLX is below $417 at expiration, the call will be worth less than the initial sale price of $17, and the short call position will profit.
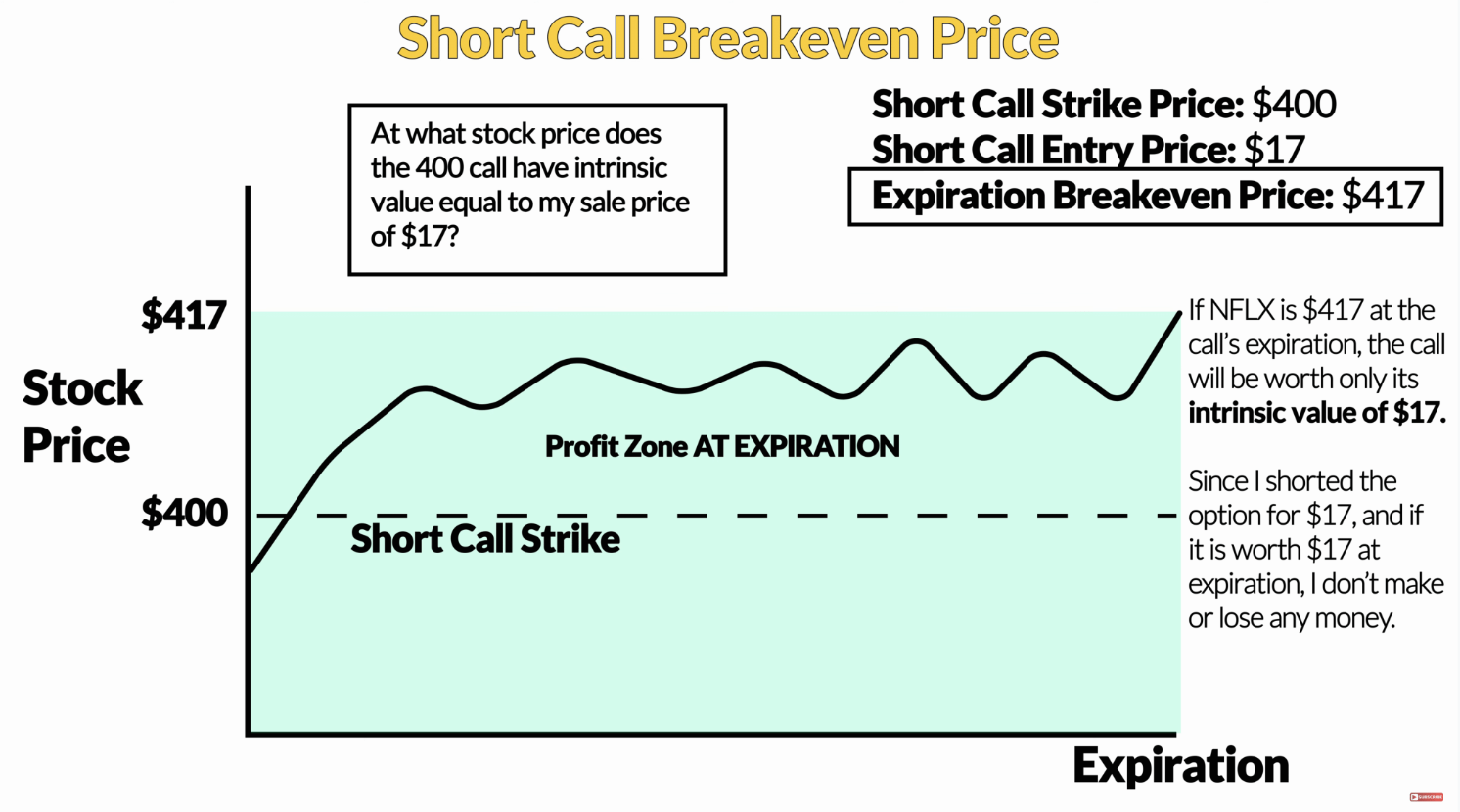
That is how it is possible to make a profit on a short call even if the stock price is higher than the call’s strike price at the expiration date.
Shorting Put Options
Thus far, we’ve talked about buying call options, buying put options, and shorting call options. Finally, we’ll be talking about shorting put options.
Similar to shorting call options, you sell the put option first and then buy it later at a lower premium (hopefully). As we know, put option prices decrease when the stock price increases, which means betting against a put option would mean betting in a stock price increase.
This is why shorting put options is a bullish trade: you profit when the stock rises and face losses when it falls.
Example
For this example, we’ll look at a put option in Activision (ATVI). On the left-hand side of the chart below, ATVI is trading at $67 per share. So let’s say I’m a trader who wants to profit from the increase in ATVI but at the same time, I’m not super sure that the stock price will increase.
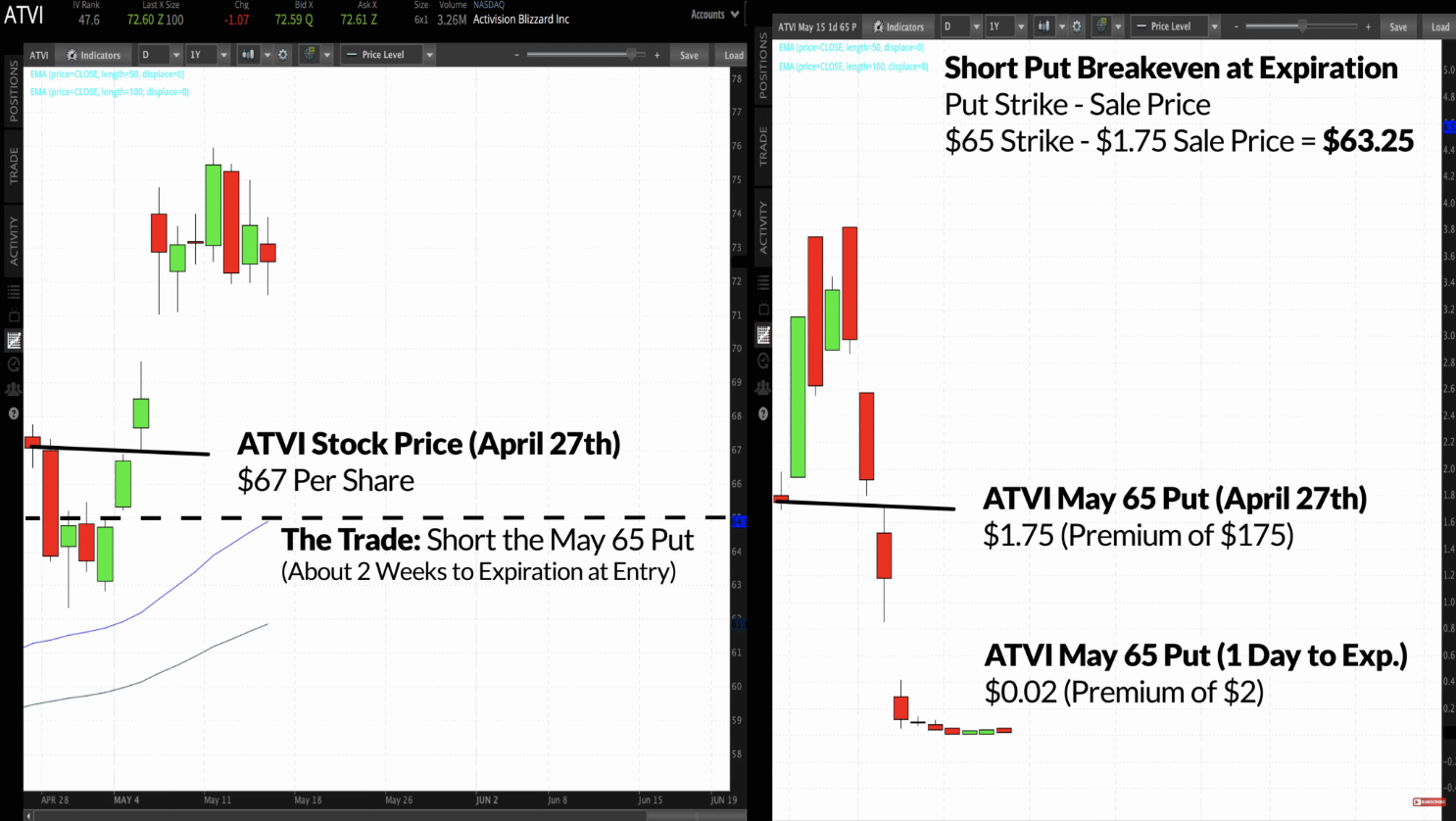
In this case, shorting put option will be one available options trade for me. And so I decide to short the May 65 put option at a premium of $175, which I collect when entering the trade. I need to buy back the put for less than $175 to make a profit.
In the left-hand chart, we can see that the stock price increased significantly by the expiration date of the put, and the put option price (right-hand chart) sank to just $0.02. This means that the option that I sold earlier at a premium of $175, I can now buy it at a premium of $2, making a profit of $173.
So that wraps it up for this part. Up until now, we’ve talked about four basic option trades: buying calls, buying puts, shorting calls and shorting puts. These four trades will make up any options trading strategy that you’ll ever see in the future. We also discussed how option prices work and the price components, and also went over terms such as In-the-money, out-of-the-money, and at-the-money.