Last updated on February 14th, 2022 , 08:27 am
3 Examples of How Time Changes Option Deltas
Understanding the definition of the Greeks in options trading (delta, theta, vega, gamma, rho) and understanding their implications are two entirely different worlds.
Why? In options trading, nothing is static. As time passes, and an options contract approaches expiration, the option Greeks are in constant motion.
To truly understand the mechanics of the Greeks, we must go deeper than simple definitions.
In this guide, we are going to explore the options Greek “delta” by illustrating how this metric reacts to various “moneyness” (in-the-money, at-the-money, and out-of-the-money) types in options trading.
Highlights
- An option’s delta compares the change in the price of a stock to the corresponding option price change.
- The delta of an in-the-money option approaches ±1 as expiration nears.
- The delta of an out-of-the-money option approaches 0 as expiration nears.
- Delta can be thought of as the percent chance an option has of expiring in-the-money.
- Since all in-the-money options are assigned and exercised at expiration for a quantity of 100 shares, the delta of an option can mirror the equivalent number of shares it represents.
Option Delta Explained
An option’s delta is a ratio that compares the change in the price of an asset (a stock in our case) to the corresponding change in the price of its derivative (an options contract). For stock/index options, delta measures an options price change relative to a $1 move in the underlying stock.
An options delta is also synonymous with the odds that a particular option has of expiring in the money.
A call option delta of +0.37 has a 37% chance of expiring in-the-money
- A put option delta of -0.60 has a 60% chance of expiring in-the-money
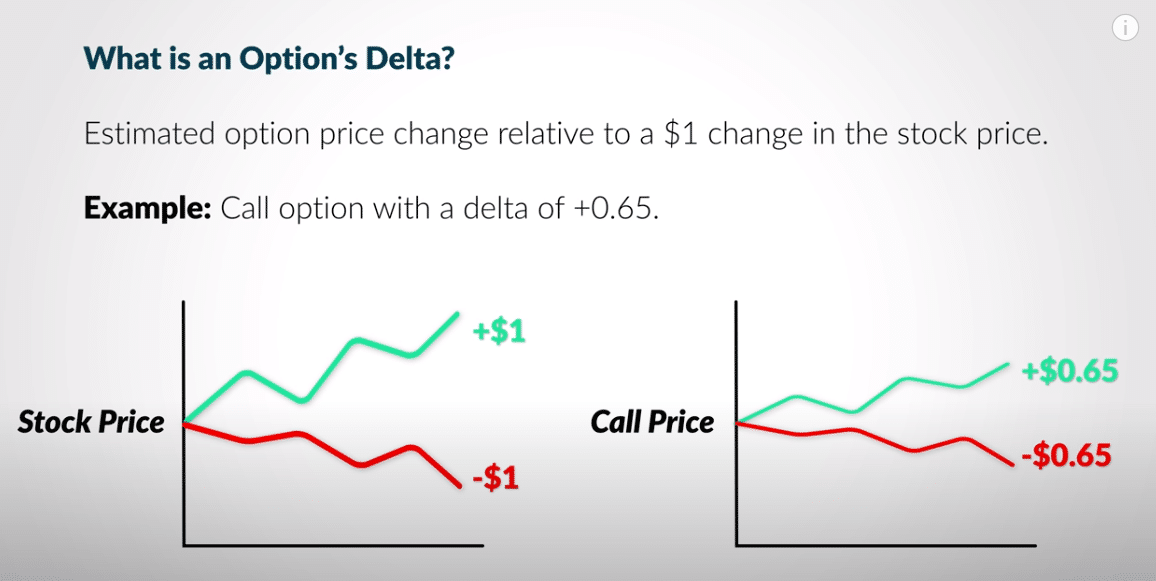
Option Delta vs Stock
The above image shows a simplified version of a call option with a delta of +0.65.
We can see that if the underlying stock price goes up by $1, our option will go up in value by .65 cents; if the underlying stock price goes down by $1, our options contract will lose .65 cents in value.
In the real world, however, the delta of an option never stays the same. It is in constant flux with the market, its value changing constantly with that of the underlying stock.
So how exactly does the value of an options delta change over time?
In this article, we are going to look at three different types of options and show how the deltas on these positions change with moves in the underlying’s implied volatility and price. Additionally, we are going to explore intuitively why these deltas are changing.
Scenario #1: Delta vs Time for In-the-Money Options
In-the-money (ITM) option deltas will approach ±1 as time passes (+1 for call and -1 for puts). This assumes that the option remains in-the-money as expiration approaches.
We can see in the above chart how an in-the-money call option with an initial delta of +0.65 approaches a positive delta of +1 as expiration nears. When an in-the-money call option expires, its delta will always be +1.
An option delta of +1 implies that an option contract will increase by $1 in value for every $1 increase in the stock’s prices. Conversely, for every $1 the stock falls in value, the option will lose $1 in value.
A delta of +1 is therefore much more sensitive in price than a delta of +0.65; the latter will only increase/decrease by 0.65 cents for a representative $1 move in the underlying stock
Two Real World Examples: In-The-Money Deltas
Let’s now take a look at what we have learned in action on the tastyworks trading platform.
E-mini S&P 500 Futures, Sept 17 4200 Call (92 days until expiration)
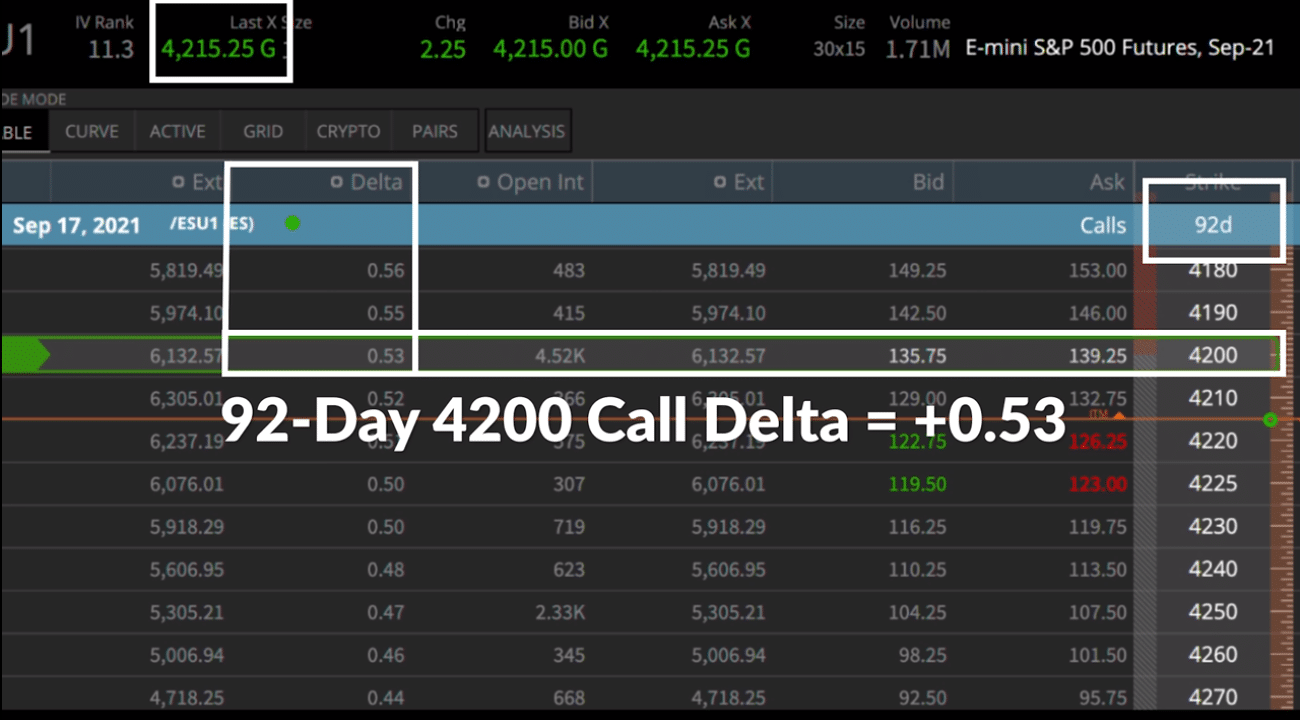
The above image (taken from the tastyworks trading platform) shows us the delta on an in-the-money call on the S&P 500 futures. The underlying is currently trading at 4215.
We have highlighted the 4200 call option expiring in September (92 days away), which is currently in-the-money by $15. The delta on this option is +0.53. This means that for every dollar the E-mini rises in value, this option contract will gain 0.53 cents in value.
So what would the option delta be on a call that is closer to expiration?
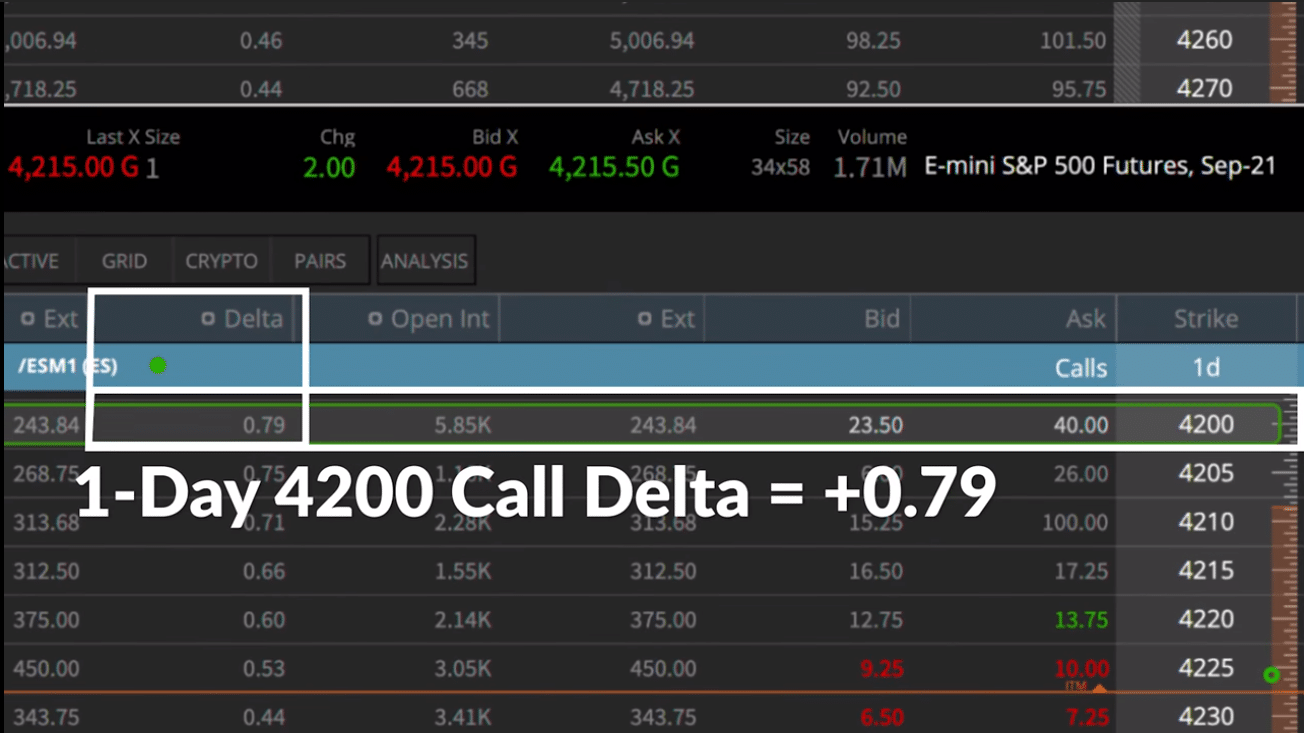
E-mini S&P 500 Futures, June 18 4200 Call (1 day until expiration)
The above image shows the option chain for the same option contract with only one difference; the expiration is no longer 92 days away, but 1 day away (June 18th). Notice how the option delta has risen in price from +0.53 (92 days until expiration) to +0.79 (1 day until expiration)?
This proves that an in-the-money options delta increases in value with the advancement of time when the underlying asset price remains constant.
Why this matters
Everything is dynamic in options trading. If you own an in-the-money option in your portfolio, this options delta will grow with the passage of time. This higher delta will make your position more sensitive and thus more vulnerable to moves in the underlying. As expiration closes in, your profit/loss will thus become more volatile.
So what about out-of-the-money options? How do they react to time and price? Let’s take a look at that one next.
Scenario #2: Delta vs Time for Out-of-the-Money Options
Out-of-the-money (OTM) option deltas will approach zero as time passes.
For example, let’s say you sell (short) a put option with 30 days until expiration with an initial delta of -.25. If in 29 days the stock price hasn’t changed, the delta of your put option will approach zero. Take a look at the image below for a visual of this change.
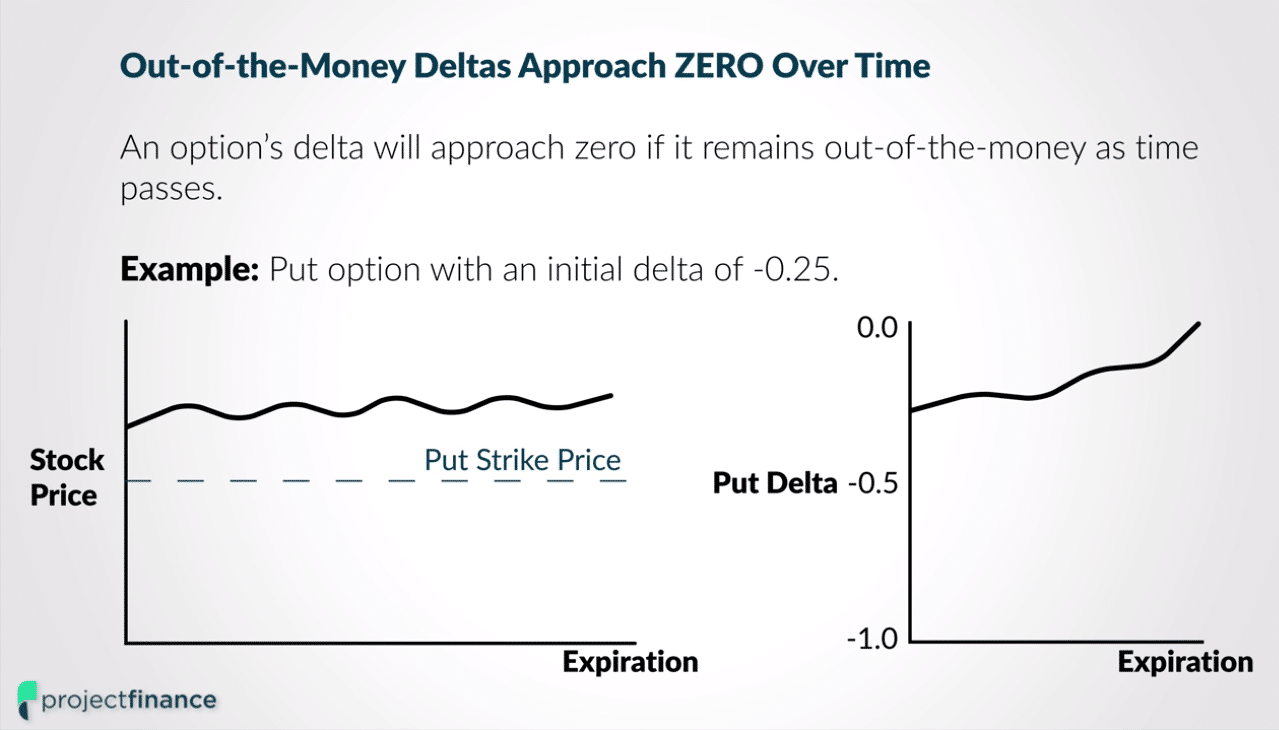
The above chart illustrates how the delta of an out-of-the-money option (assuming it remains out of the money) becomes less sensitive to moves in the underlying as time passes.
Let’s next take a look at a few real-world examples that will show us how the delta of out-of-the-money options react to changes in time and underlying price.
Two Real World Examples: Out-Of-The-Money Deltas
Apple (AAPL), July 16th 125 Put (29 days away)
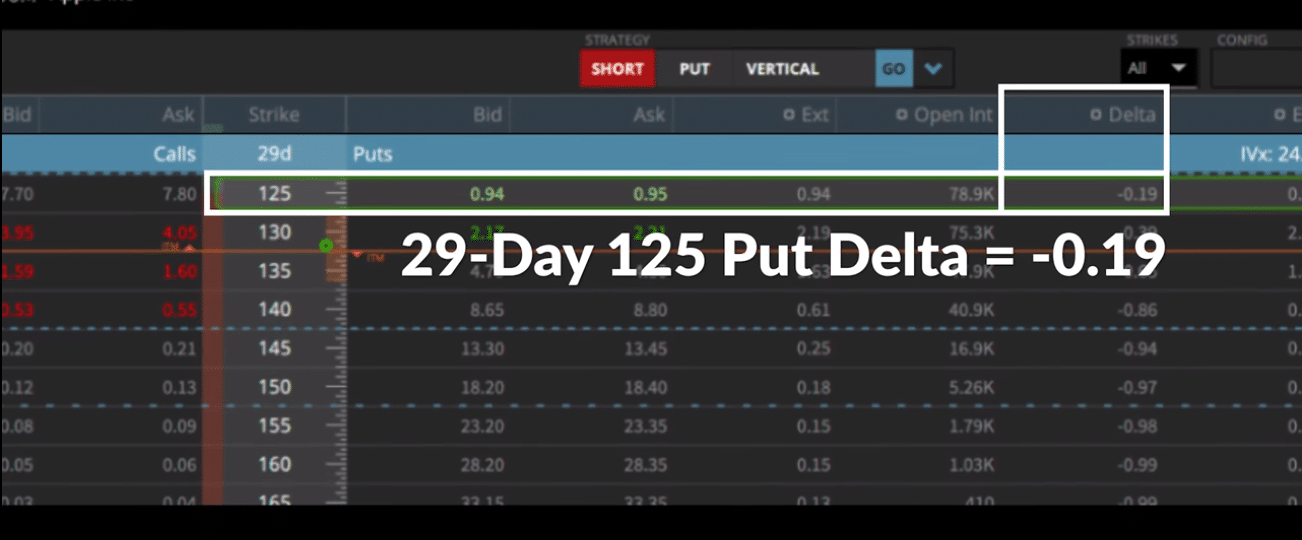
In the above image (taken from the tastyworks trading platform), we can see that the current price of AAPL is trading at 131.79. We have selected the out-of-the-money July 16th 125 put, expiring in 29 days.
The delta on this put is currently -0.19. This tells us that for every $1 increase in AAPL (all other conditions remaining constant) this option will decrease by 19 cents. Remember, since we are dealing with a put, everything is flipped on its head.
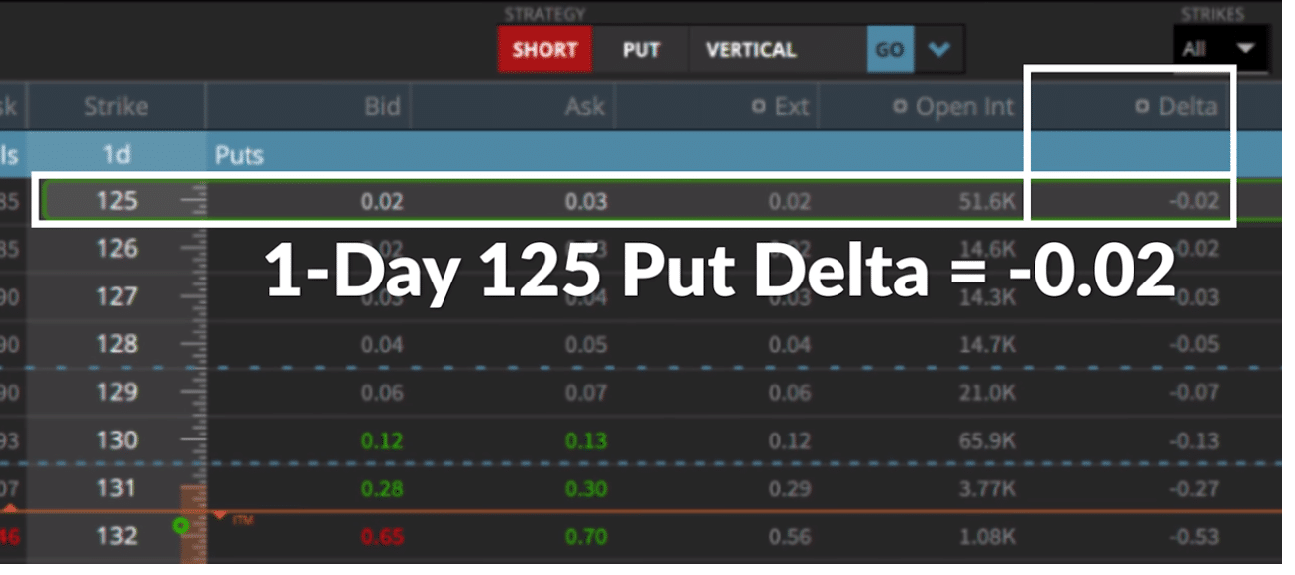
Let’s next take a look at the delta on the same option contract but of a different (closer) expiration.
Apple (AAPL), June 18th 125 Put (1 day away)
The above image shows again the 125 put on AAPL, but this time the expiration is only one day away. Notice how the option delta decreased from -0.19 to -0.02 for this expiration?
We learned before that the delta of in-the-money options increases as expiration nears; for out-of-the-money options, the exact opposite is true. The option delta for these types of options becomes less reactionary to changes in the underlying as expiration nears.
If on expiration an option remains out of the money, its value will be zero.
Why This Matters
Keeping an eye on the delta for out-of-the-money options is very important for investors. Most option traders know that an out-of-the-money option loses value as expiration approaches, but understanding how the Greeks work tells us the degree to which losses begin to mount.
For an investor long an out-of-the-money put option, rapidly decreasing deltas are not good news. This is just the opposite or an investor short a put option (as shown in our example), as they hope for time decay and invite declining deltas.
So far we have covered two types of “moneyness” options. Let’s lastly take a look at at-the-money options and see how the deltas on these types of options react to market changes.
Scenario #3: Delta vs Time for At-the-Money Options
At-the-money options will mainly have deltas close to ±0.50 prior to expiration. However, since (nearly) all options will either expire in-the-money or out-of-the-money, these types of options will converge to either ±1 or 0 as expiration approaches. Therefore, our previous examples should prove sufficient to understand how deltas change on these types of options.
How Option Deltas Trade Like Shares
We mentioned earlier that an options delta can also tell us the odds that a particular option has of expiring in the money. A call option with a delta of .75 has a 75% chance of expiring in the money.
Additionally, this percentage number can also be interpreted as the number of shares that a contract trades like. If a call option has a delta of +0.30, it has a 30% chance of expiring in-the-money, therefore, the position will almost mirror the profit/loss of 30 shares of stock.
Since out-of-the-money options lose delta over time, their share equivalent will decrease over time. For in-the-money options, their share equivalents will increase over time.
If you think about this intuitively, it should make sense. Since in-the-money options are ultimately converted to ±100 shares of stock, shouldn’t the value of in-the-money options represent this amount of shares as expiration nears?
Final Word
The delta of an option is not a fixed number, but in constant flux with even the smallest movements in the underlying implied volatility and stock price. Understanding how delta’s change over time can be a window into the health of your option positions. Without the Greeks, we are swimming in the dark.